Решение RMQ с помощью разреженной таблицы

Разреженная таблица (англ. sparse table) позволяет решать задачу online static RMQ (получение минимума или максимума на отрезке, когда элементы массива не могут изменяться, а запросы поступают последовательно) за \(O(1)\) на запрос, с предподсчётом за \(O(n log(n))\) и использованием \(O(n log(n)\) памяти.

Задача:

Дан массив \(a[1…N]\) целых чисел. Поступают запросы вида \((l,r)\), для каждого из которых требуется найти минимум среди элементов \(a[l],a[l+1],…,a[r]\).

Разреженная таблица

Разреженная таблица — двумерная структура данных \(sparse\_table[i][j]\), для которой выполнено следующее:

\(sparse\_table[i][j]=min(a[i],a[i+1],…,a[i+2^j−1]),j∈[0…log(N)]\)

Иначе говоря, в этой таблице хранятся минимумы на всех отрезках, длины которых равны степеням двойки. Объём памяти, занимаемый таблицей, равен \(O(nlog(n))\), и заполненными являются только те элементы, для которых \(i+2^j<=N\)

Простой метод построения таблицы заключён в следующем реккурентном соотношении:

Идемпотентность

Такая простота достигается за счет идемпотентности операции минимум: \(min(a,a)=a\). Это один из ключевых моментов этого метода, так как она позволяет нам корректно считать минимум в области пересечения отрезков.

Пусть ∘ — произвольная бинарная операция, которая удовлетворяет свойствам:

• ассоциативности: \(a∘(b∘c)=(a∘b)∘c\)
• коммутативности: \(a∘b=b∘a\)
• идемпотентности: \(a∘a=a\).

Утверждение

\(a_l∘a_{l+1}∘…∘a_r=(a_l∘a_{l+1}∘…∘a_{l+k})∘(a_{r−k}∘a_{r−k+1}∘…∘a_r)\) , где \(\frac{r - l}{2}⩽k⩽r−l\).

Применение к задаче RMQ

1. Состояние динамики:

   \(sparse\_table[i][j]=min(a[i],a[i+1],…,a[i+2^j−1]),j∈[0…logN]\)

2. База:

   \(sparse\_table[i][0] = a[i];\)

3. Переходы:

   \(sparse\_table[i][k] = min(sparse\_table[i][k - 1], sparse\_table[i + (1 << (k - 1))][k - 1]);\)

4. Где ответ:

   Пусть теперь дан запрос \((l,r)\). Заметим, что \(min(a[l],a[l+1],…,a[r])=min(sparse\_table[l][j],sparse\_table[r−2^j+1][j])\), где \(j = k\) где \(2^k⩽r−l+1\), то есть логарифм длины запрашиваемого отрезка, округленный вниз. Но эту величину мы уже предпосчитали, поэтому запрос выполняется за \(O(1)\).

Оптимизация

Предпосчитаем для длины отрезка \(l\) величину \(log_2(l)\). Для этого предпосчитаем массив \(fast\_log\) (от floor, т.к. логарифм округляется вниз):

vector<ll> fast_log(n + 1);
fast_log[1] = 0;
for (int i = 2; i <= n; i++) {
   fast_log[i] = floor(log2(i));
}

Вычисление \(fast\_log[l]\) происходит за \(O(log(l))\). А так как длина может принимать \(N\) различных значений, то суммарное время предпосчета составляет \(O(nlog(n))\).

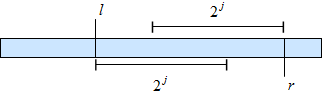
Из выше доказанной теоремы следует, что этот метод работает не только с операцией минимум, но и с любой идемпотентной, ассоциативной и коммутативной операцией. Таким образом мы получаем целый класс задач, решаемых разреженной таблицей.

Задача