Дерево отрезков¶

\(O(log(n))\) time, \(4n\) - memory

Дерево отрезков — это структура данных которая может:

за \(O(log(n))\): - нахождение значения функции на отрезке \([l, r]\)
за \(O(log(n))\) - обновление значения элемента

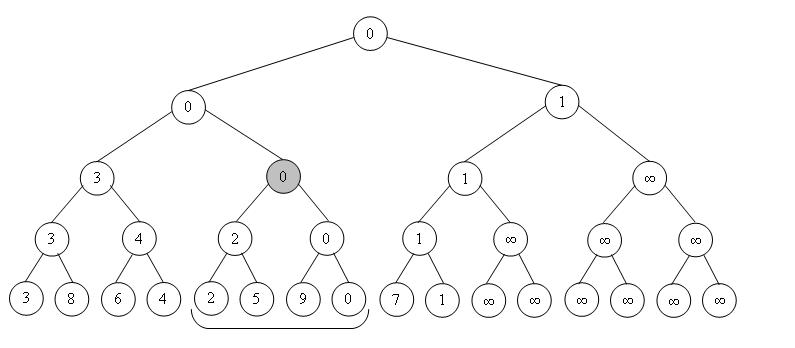
Прмер дерева на минимум:

https://neerc.ifmo.ru/wiki/images/c/c4/Segment_tree.png

Структура¶

Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по \(2\) ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива \([0…n−1]\), левый ребёнок корня содержит результат функции на \([0…\frac{n}{2}]\), а правый, соответственно результат на \([\frac{n}{2}+1…n−1]\). И так далее, продвигаясь вглубь дерева.

Построение дерева¶

Пусть исходный массив \(a\) состоит из \(n\) элементов. Для удобства построения увеличим длину массива \(a\) так, чтобы она равнялась ближайшей степени двойки, т.е. \(2^k\), где \(2^k⩾n\). Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив \(t\) из \(2^k+1\) элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой \(n+\frac{n}{2}+\frac{n}{4}…+1<2n\), где \(n=2^k\). Таким образом, структура занимает линейную память.

int size = 1 << ((int) ceil(log2(n)));

Удобно описывать эту операцию рекурсивно: мы запускаем процедуру построения от корня дерева отрезков, а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива.

Асимптотика построения дерева отрезков составит, таким образом, \(O(n)\).

Запрос суммы¶

Рассмотрим теперь запрос суммы. На вход поступают два числа \(l\) и \(r\), и мы должны за время \(O (\log n)\) посчитать сумму чисел на отрезке \(a[l \ldots r]\).

Для этого мы будем спускаться по построенному дереву отрезков, используя для подсчёта ответа посчитанные ранее суммы на каждой вершине дерева. Изначально мы встаём в корень дерева отрезков. Посмотрим, в какие из двух его сыновей попадает отрезок запроса \([l \ldots r]\) (напомним, что сыновья корня дерева отрезков — это отрезки \([0 \ldots n/2]\) и \([n/2+1 \ldots n-1]\)). Возможны два варианта: что отрезок \([l \ldots r]\) попадает только в одного сына корня, и что, наоборот, отрезок пересекается с обоими сыновьями.

Первый случай прост: просто перейдём в того сына, в котором лежит наш отрезок-запрос, и применим описываемый здесь алгоритм к текущей вершине.

Во втором же случае нам не остаётся других вариантов, кроме как перейти сначала в левого сына и посчитать ответ на запрос в нём, а затем — перейти в правого сына, посчитать в нём ответ и прибавить к нашему ответу. Иными словами, если левый сын представлял отрезок \([l_1 \ldots r_1]\), а правый — отрезок \([l_2 \ldots r_2]\) (заметим, что \(l_2 = r_1 + 1\)), то мы перейдём в левого сына с запросом \([l \ldots r_1]\), а в правого — с запросом \([l_2 \ldots r]\).

Итак, обработка запроса суммы представляет собой рекурсивную функцию, которая всякий раз вызывает себя либо от левого сына, либо от правого (не изменяя границы запроса в обоих случаях), либо от обоих сразу (при этом деля наш запрос на два соответствующих подзапроса). Однако рекурсивные вызовы будем делать не всегда: если текущий запрос совпал с границами отрезка в текущей вершине дерева отрезков, то в качестве ответа будем возвращать предвычисленное значение суммы на этом отрезке, записанное в дереве отрезков.

Иными словами, вычисление запроса представляет собой спуск по дереву отрезков, который распространяется по всем нужным ветвям дерева, и для быстрой работы использующий уже посчитанные суммы по каждому отрезку в дереве отрезков.

\(O(\log n)\) потому что \((\log n)\) высота дерева

Запрос обновления¶

Напомним, что запрос обновления получает на вход индекс \(i\) и значение \(x\), и перестраивает дерево отрезков таким образом, чтобы оно соответствовало новому значению \(a[i]=x\). Этот запрос должен также выполняться за время \(O (\log n)\).

Это более простой запрос по сравнению с запросом подсчёта суммы. Дело в том, что элемент \(a[i]\) участвует только в относительно небольшом числе вершин дерева отрезков: а именно, в \(O (\log n)\) вершинах — по одной с каждого уровня.

Тогда понятно, что запрос обновления можно реализовать как рекурсивную функцию: ей передаётся текущая вершина дерева отрезков, и эта функция выполняет рекурсивный вызов от одного из двух своих сыновей (от того, который содержит позицию \(i\) в своём отрезке), а после этого — пересчитывает значение суммы в текущей вершине точно таким же образом, как мы это делали при построении дерева отрезков (т.е. как сумма значений по обоим сыновьям текущей вершины).

Задача RSQ сумма на отрезке с обновлением одного элемента

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

vector<ll> a;
vector<ll> t;
vector<ll> p;

void build(ll v, ll l, ll r) {
    if (l == r) {
        t[v] = a[l];
        return ;
    }
    ll m = (l + r) / 2;
    build(2 * v, l, m);
    build(2 * v + 1, m + 1, r);
    t[v] = t[2 * v] + t[2 * v + 1];
}

ll get(ll v, ll l, ll r, ll A, ll B) {
    if (r < A || l > B) {
        return 0;
    }
    if (A <= l && r <= B) {
        return t[v];
    }
    ll m = (l + r) / 2;
    return get(v * 2, l, m, A, B) +
           get(v * 2 + 1, m + 1, r, A, B);
}


ll GET(ll l, ll r) {
    return get(1, 0, a.size() - 1, l, r);
}

void update(ll v, ll l, ll r, ll A, ll B, ll x) {
    if (r < A || l > B) {
        return ;
    }
    if (l == r) {
        t[v] = x;
        a[l] = x;
        return ;
    }
    ll m = (l + r) >> 1;
    update(2 * v, l, m, A, B, x);
    update(2 * v + 1, m + 1, r, A, B, x);
    t[v] = t[2 * v] + t[2 * v + 1];
}

void Set(ll i, ll x) {
    update(1,  0, a.size() - 1, i, i, x);
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    ll n;
    cin >> n;
    int size = 1 << ((int) ceil(log2(n)));
    a.resize(size);
    p.resize(2 * size, -1);
    t.resize(2 * size, 0);
    for (int i = 0; i <n; i++) {
        cin >> a[i];
    }
    build(1, 0, size - 1);
    string command;
    ll i, x;
    while (cin >> command) {
        cin >> i >> x;
        if (command == "sum") {
            cout << GET(i - 1, x - 1) << "\n";
        } else {
            Set(i - 1, x);
        }
    }
    return 0;
}

Обновление значений на отрезке [l, r] за \(O(log(n))\)¶

TODO